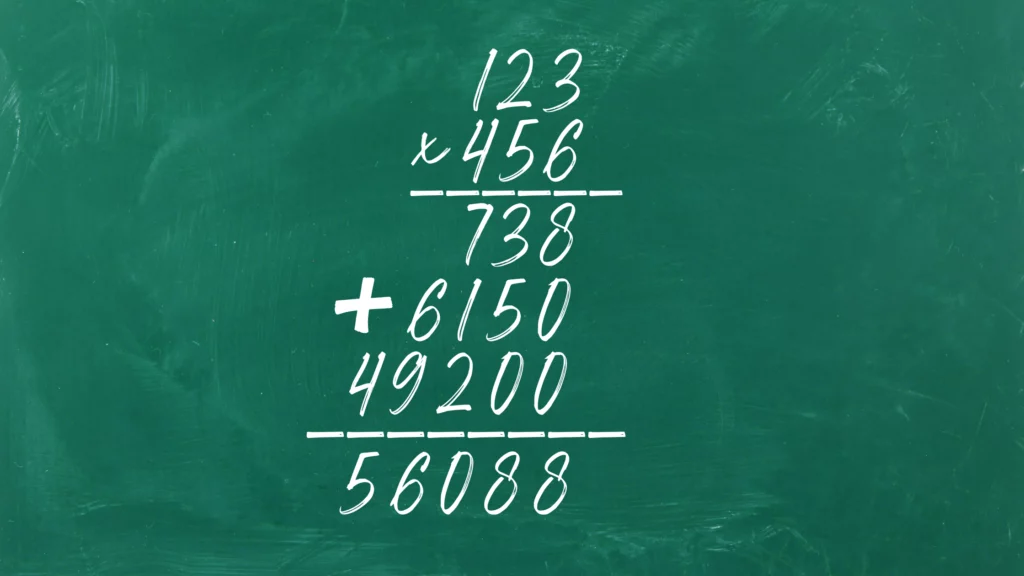En este post de Editorial Edarca te explicamos las multiplicaciones de tres cifras. Cuando aprendes a multiplicar por tres cifras, multiplicar por más dígitos se hace más fácil, ya que siempre se sigue el mismo mecanismo. Esperamos que después de leer este artículo entiendas cómo se hace y te sea mucho más fácil.
Cuando multiplicamos números de tres cifras, ordenamos los números en columnas de acuerdo con los valores posicionales. Sabemos que los números de tres cifras están ordenados según su valor posicional como unidades, decenas y centenas.
Una vez que tenemos un conjunto de dos números para multiplicar, generalmente mantenemos el número mayor arriba y el menor debajo. El número que se coloca encima se convierte en el multiplicando y el número escrito debajo es el multiplicador.
Cuando los números se ordenan según su valor posicional, multiplicamos el multiplicador con todos los dígitos del multiplicando uno por uno comenzando desde el dígito de las unidades, seguido por el dígito de las decenas y luego el dígito de las centenas. Todos estos productos se escriben juntos y dan como resultado el producto final.
Por ejemplo, si necesitamos multiplicar 123 × 3, los colocamos como mostramos a continuación:
Donde 123 es el multiplicando y 3 es el multiplicador. Después de multiplicar estos números obtenemos el producto 269.
Pasos para las multiplicaciones de tres cifras
Ejemplo:
Multiplicar 123 por 456.
Paso 1:
Organiza los números 123 y 456 en columnas según sus valores posicionales.
Paso 2:
Multiplica 6 por cada cifra de 123.
Cuando multiplicamos 6 por 3, obtenemos 18. Como 18 es un número de 2 dígitos, escribimos 8 debajo de la columna de las unidades y llevamos 1 a la columna de las decenas, encima del 2.
Cuando multiplicamos 6 por 2, obtenemos 12. Ahora, sumamos el 1 arrastrado a 12 y obtenemos 13. Como 13 es un número de 2 dígitos, escribimos 3 debajo de la columna de las decenas y llevamos 1 a la siguiente columna, encima del 1.
Cuando multiplicamos 6 por 1, obtenemos 6. Ahora, sumamos el 1 arrastrado a 6 para obtener 7. Como no queda ningún otro dígito para la multiplicación, escribimos 7. Entonces, tenemos 738 en la primera línea como producto parcial.
Paso 3:
Ahora, coloca un cero debajo de este producto parcial en la columna de las unidades. Esto se debe a que en este paso en realidad estamos multiplicando 123 por 50.
Paso 4:
Multiplica 5 por cada cifra de 123.
Cuando se multiplica 5 por 3, obtenemos 15. Como 15 es un número de 2 cifras, escribimos 5 en la columna de las decenas y llevamos 1 a la siguiente columna encima de 2.
Cuando multiplicamos 5 por 2, obtenemos 10. Ahora, sumamos el 1 arrastrado a 10 para obtener 11. Como 11 es un número de 2 dígitos, escribimos 1 en la columna de centenas y llevamos 1 a la siguiente columna encima de 1.
Cuando multiplicamos 5 por 1, obtenemos 5. Ahora, sumamos el 1 arrastrado a 5 para obtener 6. Como no queda ningún otro dígito para la multiplicación, escribimos 6. Entonces, tenemos 6150 en la segunda línea del producto parcial.
Paso 5:
Ahora, coloca dos ceros (0) debajo de la columna de las unidades y las decenas debajo del producto parcial obtenido en el paso anterior. Esto se debe a que en este paso en realidad estamos multiplicando 123 por 400.
Paso 6:
Multiplicamos 4 por cada dígito de 123.
Cuando multiplicamos 4 por 3, obtenemos 12. Como 12 es un número de 2 dígitos, escribimos 2 debajo de la columna de las centenas y llevamos 1 a la siguiente columna encima de 2.
Cuando multiplicamos 4 por 2, obtenemos 8. Ahora, sumamos el 1 arrastrado a 8 para obtener 9. Escribimos 9 en la siguiente columna.
Cuando multiplicamos 4 por 1, obtenemos 4. Como no queda ningún otro dígito para la multiplicación, escribimos 4. Entonces, tenemos 49200 en la tercera línea como producto parcial.
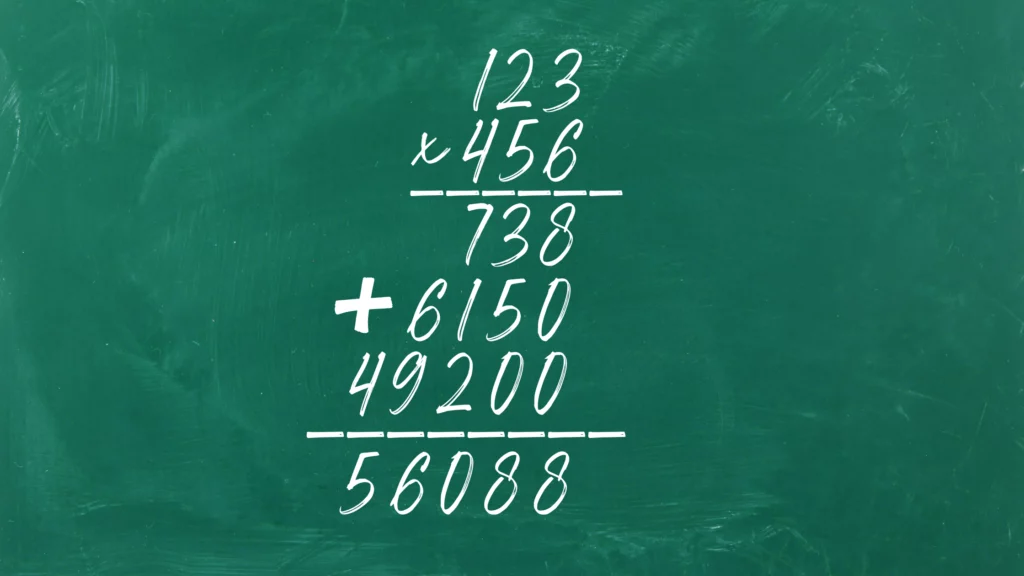
Paso 7:
Agrega los 3 productos parciales para obtener el producto final. Esto significa 738 + 6150 + 49200 = 56088.
Por lo tanto, el producto final es 56.088.
 Cuadernos Lengua valenciana 3 primaria - Fem Pinya
1 × 36,00€
Cuadernos Lengua valenciana 3 primaria - Fem Pinya
1 × 36,00€  Grama ágil 3 - Cuaderno de gramática - 3º de Primaria
1 × 11,00€
Grama ágil 3 - Cuaderno de gramática - 3º de Primaria
1 × 11,00€  Colección Cuadernos de Ortografía - Punto y Aparte serie verde - primaria
1 × 12,00€
Colección Cuadernos de Ortografía - Punto y Aparte serie verde - primaria
1 × 12,00€  Cuaderno de velocidad y comprensión lectora - Lector 15 - primaria
1 × 1,50€
Cuaderno de velocidad y comprensión lectora - Lector 15 - primaria
1 × 1,50€  Cuaderno de grafomotricidad - Puente Infantil - Números 3 años
1 × 5,00€
Cuaderno de grafomotricidad - Puente Infantil - Números 3 años
1 × 5,00€